
In the simple linear regression model, the \(x_i\) are assumed to be fixed, known constants, and are thus notated with a lower case variable.Many datasets contain multiple quantitative variables, and the goal of an analysis is often to relate those variables to each other. Since we will have \(n\) observations, we have \(n\) random variables \(Y_i\) and their possible values \(y_i\). Recall that we use capital \(Y\) to indicate a random variable, and lower case \(y\) to denote a potential value of the random variable. We are now using \(Y_i\) and \(x_i\), since we will be fitting this model to a set of \(n\) data points, for \(i = 1, 2, \ldots n\). We have slightly modified our notation here. This model has three parameters to be estimated: \(\beta_0\), \(\beta_1\), and \(\sigma^2\), which are fixed, but unknown constants. That is, the \(\epsilon_i\) are independent and identically distributed (iid) normal random variables with mean \(0\) and variance \(\sigma^2\). We now define what we will call the simple linear regression model, We will write our model using \(\beta_1\) for the slope, and \(\beta_0\) for the intercept, With this in mind, we would like to restrict our choice of \(f(X)\) to linear functions of \(X\). There is still some variation about this line, but it seems to capture the overall trend. As speed increases, the distance required to come to a stop increases. The line on the plot below seems to summarize the relationship between stopping distance and speed quite well. Lastly, we could try to model the data with a well-chosen line rather than one of the two extremes previously attempted. (Note that in this example no function will go through every point, since there are some \(x\) values that have several possible \(y\) values in the data.) The stopping distance for a speed of 5 mph shouldn’t be off the chart! (Even in 1920.) This is an example of overfitting. This also doesn’t seem to work very well. We could also try to model the data with a very “wiggly” function that tries to go through as many of the data points as possible. The obvious fix is to make the function \(f(X)\) actually depend on \(x\). Many of the data points are very far from the orange line representing \(c\). (Some function \(f(X) = c\).) In the plot below, we see this doesn’t seem to do a very good job. That is, the model for \(y\) does not depend on the value of \(x\).

We could try to model the data with a horizontal line. What sort of function should we use for \(f(X)\) for the cars data? You could think of this a number of ways:
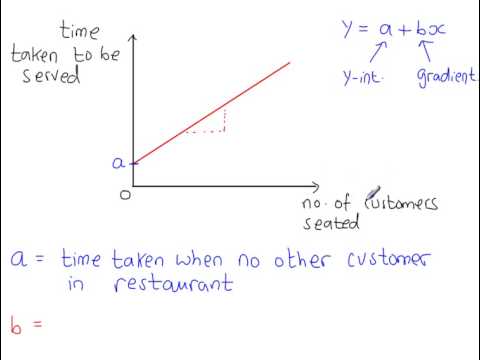
This indicates that if we plug in a given value of \(X\) as input, our output is a value of \(Y\), within a certain range of error. The function \(f\) describes the functional relationship between the two variables, and the \(\epsilon\) term is used to account for error. In the cars example, we are interested in using the predictor variable speed to predict and explain the response variable dist.īroadly speaking, we would like to model the relationship between \(X\) and \(Y\) using the form For example, when trying to predict a person’s weight given their height, would it be accurate to say that height is independent of weight? Certainly not, but that is an unintended implication of saying “independent variable.” We prefer to stay away from this nomenclature. While these other terms are not incorrect, independence is already a strictly defined concept in probability. However, those monikers imply mathematical characteristics that might not be true. Other texts may use the term independent variable instead of predictor and dependent variable in place of response. The predictor variable is used to help predict or explain the response (target, outcome) variable, \(y_i\). We use \(x_i\) as the predictor (explanatory) variable. We use \(i\) as an index, simply for notation. We have pairs of data, \((x_i, y_i)\), for \(i = 1, 2, \ldots n\), where \(n\) is the sample size of the dataset. Plot(dist ~ speed, data = cars, xlab = "Speed (in Miles Per Hour)", ylab = "Stopping Distance (in Feet)", main = "Stopping Distance vs Speed", pch = 20, cex = 2, col = "grey") 17.3.6 Confidence Intervals for Mean Response.16 Variable Selection and Model Building.14.2.5 poly() Function and Orthogonal Polynomials.14.1.1 Variance Stabilizing Transformations.



 0 kommentar(er)
0 kommentar(er)
